- Introduction
- Configuration
- Dessiner
- Ajouter du
bordelmouvement - Les quatre concepts fondamentaux de la programmation
- 1-concept-no-1-les-methodes
- Concept no.2 : Les variables
- Concept no.3 : Les boucles
- Concept no.4 : Les bifurcations
- Pong
- Images-photographiques
- Typographie
- bibliotheques-externes
- ddd
- Chanter|Gueuler
- Arduino-Wiring
- Listes
- Programmation orientée-objet
- Hypermedia Processing Libraries
Nous avons vu jusqu’ici un certain nombre de méthodes permettant de dessiner des images en deux dimensions. La plupart s’inspirent de la logique proposé par John maeda dans son livre+langage Design by Numbers : un stylo dessine sur une feuille de paper. On efface le paper en définissant son background(r, v, b), on tire un trait en dessinant une line(x1, y1, x2, y2).
Processing permet de facilement basculer tout ce travail en trois dimensions. On continue à dessiner des cercles, des triangles, des lignes, des carrés, mais au lieu de les dessiner sur un papier à plat en 2-dimensions, on les dessinent à l’intérieur d’une volume en 3 dimensions.
On hérite donc des logiques apprises jusqu’ici, c’est juste l’espace qui se transforme autour de notre dessin. C’est d’ailleurs une excellente façon d’apprendre la logique de construction d’une image en trois dimensions, car les logiques 3d de Processing ne diffèrent pas des logiques des logiciels de modélisation, ni des cartes graphiques elles-mêmes qui rendent l’image visible.
Définir l’espace du dessin
La première chose à faire si on veut dessiner en 3d, c’est de déclarer à Processing que nous allons utiliser l’espace 3d du système, et non pas son espace 2d. On ne va pas dessiner sur une pseudo-feuille de paper, mais dans un espace tridimensionnel. Il suffit alors, lors de la déclaration de la taile de l’animation, de rajouter P3D et le tour est joué :
size(200,200,P3D);Avec cette “annonce” qu’on sera désormais en 3d, de nouvelles méthodes s’offrent à nous, mais qui nécessitent de bien comprendre leur logique.
Illustration
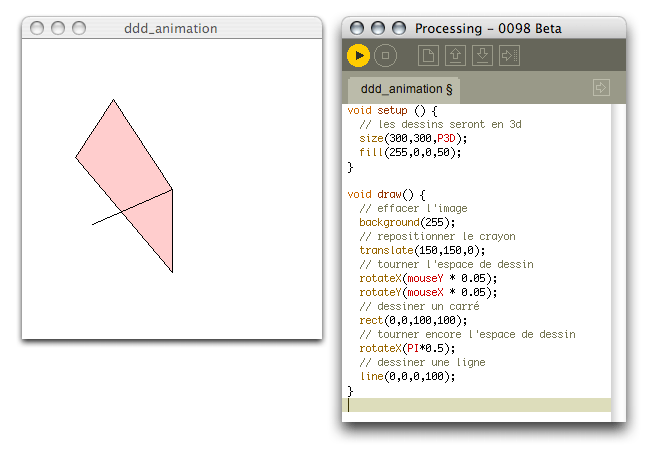
Il est difficile, dans un tutorial en ligne, de faire des illustrations de dessins en 3d. Une illustration interactive pourrait peut-être nous aider. Je vous demanderai donc de copier le code suivant dans Processing et de le jouer ; juste pour s’habituer aux formes que nous allons apprendre à dessiner. Si vous ne comprenez pas les nouveaux termes (i.e. translate() et rotate()) ce n’est pas grâve, je les expliquerai dans un instant. J’aimerais juste que vous ayez sous les yeux, un exemple concret d’une image 3d :
void setup () {
// les dessins seront en 3d
size(300,300,P3D);
fill(255,0,0,50);
}
void draw() {
// effacer l'image
background(255);
// repositionner le crayon
translate(150,150,0);
// tourner l'espace de dessin
rotateX(mouseY * 0.05);
rotateY(mouseX * 0.05);
// dessiner un carré
rect(0,0,100,100);
// tourner encore l'espace de dessin
rotateX(PI*0.5);
// dessiner une ligne
line(0,0,0,100);
}
Transformations : orienter le crayon
Deux concepts sont essentiels pour comprendre ce qui se passe dans notre illustration : le repositionnement et la réorientation. Ce sont des transformations qui modifient l’espace de dessin lui-même. On peut aussi décrire ces transformations à l’inverse et dire qu’il s’agit des transformations du crayon qui dessineront la figure dans cet espace. Car dans le P3D vous pouvez imaginer ces transformations comme si, avant de dessiner mon rectangle, je changeais la position de mon stylo et faisais une rotation de ma main. Si ma main n’était donc pas à plat vis-à-vis de l’écran — si elle était inclinée — tous mes dessins serait inclinés en conséquence. Autrement dit, je continue à dessiner des formes simples — rectangles, cercles, etc. — mais ma position dans l’espace a changé, ainsi que son orientation.
C’est un procédé un peu étrange, parce qu’en réalité nous ne pouvons évidemment pas dessiner dans l’espace de cette façon. Je ne peux pas mettre ma main dans l’air à l’endroit voulu et dessiner un rectangle, à moins que je sois malin comme Yves Klein, et je demande de l’or en échange :

Et pourtant dans le mode P3D c’est exactemment ce que vous allez faire. Vous allez positionner votre main à l’endroit où vous voulez dessiner (tiens un peu plus à gauche, un peu plus haut, maintenant incliné sur l’axe x à 132°, …) puis dessiner la forme. Imaginez donc que vous dessinez des formes dans l’air, comme [Yves Klein](https://fr.wikipedia.org/wiki/Yves Klein).
Ces positionements s’appelle des transformations et sont manipulés par 3 différentes méthodes dans Processing : translate, rotate, et scale. Nous ne traiterons pas scale cette fois-ci, mais sachez qu’il s’agit d’une des transformations possibles du crayon avant qu’il dessine. (Au fait, nous ignorons la transformation scale parce qu’il brouille notre métaphore foireux d’un crayon dans l’espace. Plutôt que de choisir un meilleur métaphore, il est plus simple d’ignorer tout simplement son existence. Bon, il est parti. On peut resortir.)
Ensuite, il nous reste les méthodes translate et rotate, essentielles pour les formes 3d. La transformation translate permet de repositionner le crayon dans l’espace, puis la transformation rotate permet d’incliner le crayon dans l’espace. Sans ces deux transformations, nous aurions du mal à dessiner des formes.
Translation
La méthode translate ne se traduit pas bien en français, car il s’agit au fait d’un déplacement et non pas d’une traduction. La méthode translate sert à replacer le point 0,0 de la feuille, autrement dit, le point d’origine du dessin, autrement dit le point de départ du crayon. Il s’écrit en définissant les déplacements x, y, z du crayon :
translate( 100, 100, 0);Perdu ? Regardez l’exemple suivant :
size(200,200,P3D);
background(255);
// dessiner un cercle au point 0,0
ellipse(0,0,50,50);
// bouger notre crayon (déplacement)
translate(100,100,0);
// dessiner un cercle au point 0,0
ellipse(0,0,50,50);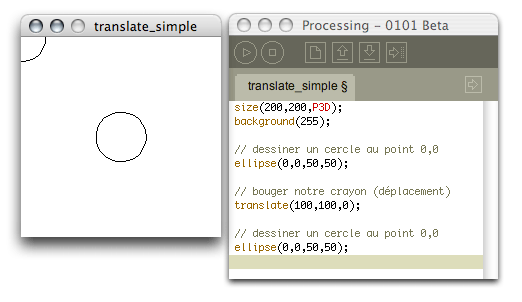
Nous avons deux cercles, dessinés avec exactement la même formule : ellipse(0,0,50,50);. Ces deux méthodes dessinent des cercles d’un diamètre de 50 pixels sur le point 0,0 de la fenêtre. mais comme nous pouvons voir dans l’illustration, le deuxième cercle est dessiné en plein milieu de la fenêtre. Pourquoi? Parce que nous avons redéfini le point 0,0 de la fenêtre : elle est dorénavant au milieu de la fenêtre au point 100,100. C’est-à-dire qu’avant de dessiner le deuxième cercle, nous avons bougé notre crayon dans l’espace. Tous les dessins se feront à partir maintenant du point 100,100, au lieu du point 0,0 comme auparavant.
À noter: nous n’avons pas encore utilisé une translation sur l’axe z, c’est-à-dire un mouvement de profondeur à l’intérieur de l’écran ou à l’inverse vers le spectateur. Si on choisit une translation d’une valeur -100 sur l’axe z, par exemple, le crayon se placera à 100 pixels de distance à l’intérieur de la fenêtre, et dessinera le cercle là-bas. C’est-à-dire que le cercle serait tout petit.
Rotation
Les méthodes de rotation, c’est-à-dire de réorientation du crayon dans l’espace 3d, sont très complémentaires à la méthode translate(x, y, z). Au lieu de déplacer le point 0,0 de l’espace, on réoriente l’espace autour du point 0,0.
Huh? Keskiviendedire? Voici un exemple que je vous invite à copier pour mieux comprendre cette idée :
void setup() {
size(200,200,P3D);
nofill();
background(255);
rect(0,0,150,150);
rotateZ(PI * 0.25);
rect(0,0,150,150);
}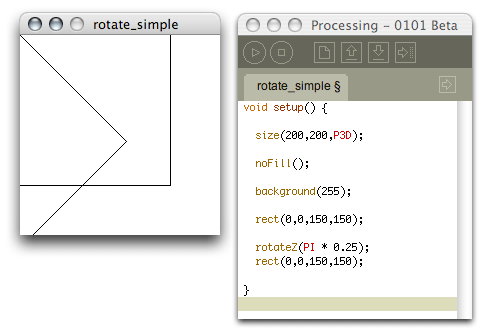
Notez que dans notre illustration nous avons dessiné deux fois le même carré avec la méthode rect(0,0,150,150). Ces deux carrés devrait se dessiner donc du point 0,0 jusqu’au point 150,150, n’est-ce pas ? mais évidemment ce n’est pas ce qui s’est passé, vu le résultat. Car entre les deux méthodes, nous avons réorienté notre crayon : nous avons fait une sorte de rotation de notre main avant de dessiner le deuxième carré. Du coup ce deuxième carré se dessine incliné, car tout dessin à partir de ce point sera affecté par notre rotation sur l’axe z.
Radians
Notez également dans l’illustration précédente qu’en définissant la valeur de rotation de PI * 0.25 nous avons en réalité fait une rotation de 45° du carré. Dans Processing vous définissez toujours des rotations avec ce qu’on appelle des radians, et non pas avec des degrés. PI = 180°. 2 * PI = 360°. Autremment dit, et pour donner une petite règle simple : une rotation d’un demi-cercle, c’est-à-dire 180° s’écrit rotateZ(PI) ou rotateZ(3.1415) — c’est comme vous voulez. Si vous voulez faire une rotation de 90°, vous écrivez rotateZ(PI * 0.5) et si vous voulez faire une rotation de 45° vous écrivez rotateZ(PI * 0.25).
Les trois axes (du mal, du bien, peu importe)
Avant d’avancer plus loin, une petite digression s’impose sur les axes de rotation. Tout le monde comprend probablement qu’une translation sur l’axe x fait bouger le crayon horizontalement, qu’une translation sur l’axe y fait bouger le crayon veritcalement, et qu’une translation sur l’axe z fait bouger le crayon en profondeur — à l’intérieur de l’écran ou vers l’utilisateur. mais il est plus difficile souvent de comprendre intuitivement les rotations.
Regardez l’exemple plus haut : nous avons indiqué que la rotation se fera autour de l’axe z. maintenant regardez l’illustration suivante et imaginez que le carré doit tourner autour de l’axe z, c’est-à-dire de l’axe qui descend dans l’écran en profondeur.
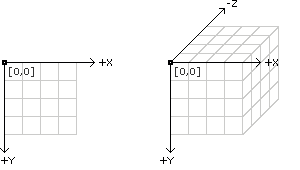
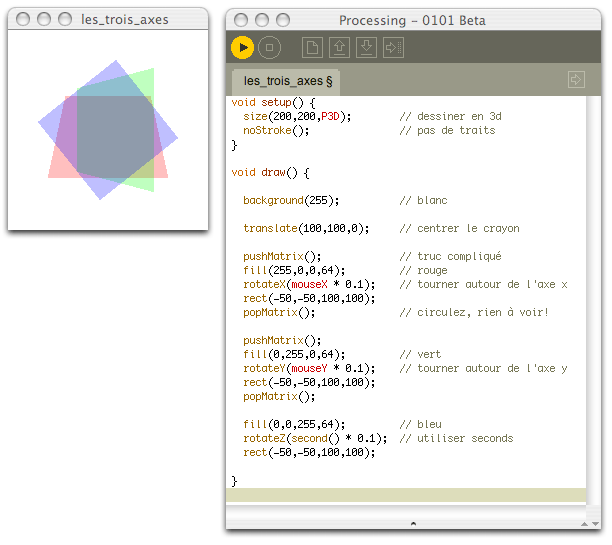
Les rotations se font donc autour d’un axe x, y, z ou d’une combination des trois. Dans l’exemple suivante nous avons créé une petite animation interactive pour rendre plus clair ces rotations. Copiez ce programme dans Processing et lancez-la (même si vous ne comprennez pas toutes les termes) :
void setup() {
size(200,200,P3D); // dessiner en 3d
noStroke(); // pas de traits
}
void draw() {
background(255); // blanc
translate(100,100,0); // centrer le crayon
pushmatrix(); // truc compliqué
fill(255,0,0,64); // rouge
rotateX(mouseX * 0.1); // tourner autour de l'axe x
rect(-50,-50,100,100);
popmatrix(); // circulez, rien à voir!
pushmatrix();
fill(0,255,0,64); // vert
rotateY(mouseY * 0.1); // tourner autour de l'axe y
rect(-50,-50,100,100);
popmatrix();
fill(0,0,255,64); // bleu
rotateZ(second() * 0.1); // tourner autour de l'axe z
rect(-50,-50,100,100);
}
Box & Sphere
On comprends beaucoup mieux l’importance du couple translate et rotate avec deux nouvelles formes que Processing met à notre disposition dans l’espace 3d : box (une boite) et sphere (une sphère). Car box et sphere ne peuvent se dessiner que sur le point 0,0 : il n’y a pas — contrairement à rect(), line(), ou ellipse() — la possibilité de définir l’emplacement x, y, ou z du dessin. Il s’écrit toujours à l’endroit 0,0 de la fenêtre. Si vous voulez le dessiner ailleurs, il faut déplacer le crayon avant avec la méthode translate().
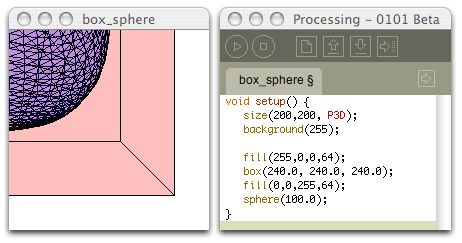
Nous avons deux très joilies formes : une boîte rouge et une sphère (formée de petites triangles) bleue. Sauf que, comme je viens de dire, on ne peut pas donner d’emplacement autre pour ces formes que le point 0,0 de la fenêtre. Du coup les formes débordent en ne se voient qu’à moitié.
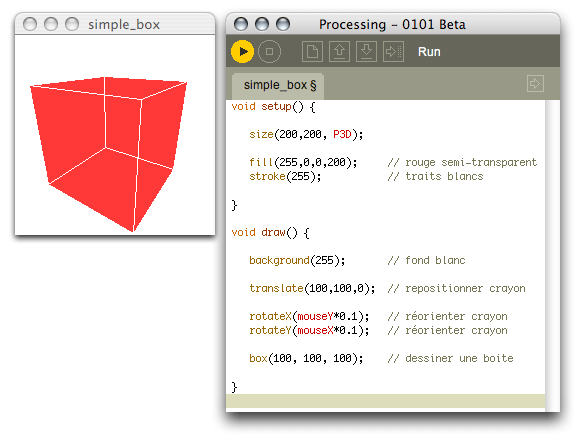
Pour dessiner une boîte au milieu de l’écran (voire où on veut) il faut obligatoirement repositionner le crayon avec la méthode translate(x, y, z) :
void setup() {
size(200,200, P3D);
fill(255,0,0,200); // rouge semi-transparent
stroke(255); // traits blancs
}
void draw() {
background(255); // fond blanc
translate(100,100,0); // repositionner crayon
rotateX(mouseY*0.1); // réorienter crayon
rotateY(mouseX*0.1); // réorienter crayon
box(100, 100, 100); // dessiner une boite
}
Accumulation des transformations
Nous dessinons des forms en trois dimensions en plaçant notre crayon à un endroit donné, en l’orientant, puis en dessinant des formes simples (carrés, triangles, cercles, lignes). Il est important du coup de noter que ces transformations sont additives : c’est-à-dire qu’une transformation du crayon dans l’espace transformera par la suite l’ensemble des transformations suivantes.
Voici une animation complexe que je vous recommande de nouveau à copier dans Processing et observer en fonctionnement :
void setup() {
size(200,200,P3D);
fill(128,128,128,128);
}
void draw() {
// fond blanc
background(255);
// commencer au centre de la fenêtre
translate(100,100,0);
// tourner le crayon avec la souris
rotateX(mouseY*0.1);
rotateY(mouseX*0.1);
// dessiner une boite
stroke(0);
box(25.0, 25.0, 25.0);
// tracer une ligne
stroke(255,0,0);
line(0,0,75,0);
// se déplacer au bout de la ligne
translate(75,0,0);
// dessiner une sphère
stroke(0,0,0,3);
sphere(10.0);
}Ce code devra dessiner la forme interactive suivante :
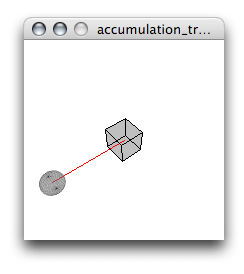
Observez dans cette illustration comment les transformations s’enchaînent les unes sur les autres :
- d’abord on se met au centre
- (à partir de cette position) on fait une rotation sur l’axe
x - (à partir de ces deux transformations) on fait une rotation sur l’axe
y - on dessine une boîte
- on dessine une ligne
- (à partir des précédentes transformations) on se déplace sur l’axe
x - finalement on dessine une sphère
Les transformations de l’espace, autrement dit le repositionnement du crayon dans cet espace, s’enchaînent et influence à leur tour tous les dessins et toutes les transformations qui s’en suivent.
Ajouter des transformations
Comment faire si, du coup, nous voulons dessiner deux lignes et deux satellites à partir du centre, comme dans l’illustration suivante:
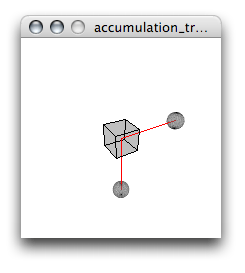
Comme les transformations s’additionnent les unes sur les autres ce dessin pourrait venir devenir compliqué. Par exemple, si on essaie de dessiner une ligne+sphère puis une autre, comme dans le code suivant, nous nous trouverons avec une figure étrange (mais pas sans intérêt) :
void setup() {
size(200,200,P3D);
fill(128,128,128,128);
}
void draw() {
// fond blanc
background(255);
// commencer au centre de la fenêtre
translate(100,100,0);
// tourner le crayon avec la souris
rotateX(mouseY*0.1);
rotateY(mouseX*0.1);
// dessiner une boite
stroke(0);
box(25.0, 25.0, 25.0);
// tracer une ligne
stroke(255,0,0);
line(0,0,75,0);
// se déplacer au bout de la ligne
translate(75,0,0);
// dessiner une sphère
stroke(0,0,0,3);
sphere(10.0);
// tracer une deuxième ligne
stroke(255,0,0);
line(0,0,0,75);
// se déplacer au bout de la ligne
translate(0,75,0);
// dessiner une sphère
stroke(0,0,0,2);
sphere(10.0);
}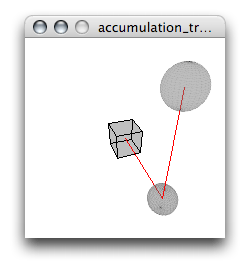
Comme les transformations sont additives la deuxième ligne s’est additionné sur le dos de la première transformation.
On aurait pu — une fois que nous avons dessiné la première satellite — revenir en arrière en recalculant la transformation à l’envers. mais qui veut faire un tel travail ?
Revenir en arrière
Pour nous aider, voici qu’arrive dans notre arsenal deux nouvelles fonctions assez magiques : pushmatrix() et popmatrix(). Ces deux fonctions permettent de créer une sorte de marque-page à l’endroit d’une transformation (se souvenir de cette position), nous facilitant le retour à cette position une fois terminé d’autres transformations plus compliquées.
On peut dessiner enfin notre carré, se souvenir de sa position+orientation, aller dessiner la satellite numéro un, retourner à la position du carré, puis aller dessiner la satellite numéro deux.
Voici le programme :
void setup() {
size(200,200,P3D);
fill(128,128,128,128);
}
void draw() {
// fond blanc
background(255);
// commencer au centre de la fenêtre
translate(100,100,0);
// tourner le crayon avec la souris
rotateX(mouseY*0.1);
rotateY(mouseX*0.1);
// dessiner une boite
stroke(0);
box(25.0, 25.0, 25.0);
// tracer une ligne
stroke(255,0,0);
line(0,0,75,0);
// se souvenir de cette position/orientation
pushmatrix();
// se déplacer au bout de la ligne
translate(75,0,0);
// dessiner une sphère
stroke(0,0,0,3);
sphere(10.0);
// revenir à la précedente position/orientation
popmatrix();
// tracer une deuxième ligne
stroke(255,0,0);
line(0,0,0,75);
// se déplacer au bout de la ligne
translate(0,75,0);
// dessiner une sphère
stroke(0,0,0,2);
sphere(10.0);
}Avec ce programme nous arrivons enfin à la figure que nous cherchions depuis le début :

Regardez ligne-par-ligne ce programme, il est important. Et en lisant chaque ligne imaginez-vous en train de placer votre crayon virtuel à l’intérieur de l’espace abstrait de l’écran 3d.
La clé de ce programme est le pushmatrix() qui permet de se souvenir de la position/orientation du carré pour ensuite revenir à cette position/orientation avec la méthode popmatrix().
pushmatrix() et popmatrix() permettent donc d’enregistrer des transformations et d’y revenir. Ils peuvent même enregistrer plusieurs transformations les unes à la suite des autres, et d’y revenir en arrière de la même mannière.
Push? Pop?
Quand j’étais gamin on mangeait des glaces à base de yaourt appelés des Pushpops :

mais finalement ces glaces n’ont rien à voir avec ce qu’on traite ici. Donc oubliez-les. Non, finalement le métaphore de push et pop concerne un tout autre souvenir d’enfance, moins agréable celui-ci : la cantine de l’école. Et ici je suis sûr que même certains français ont connu ce système :

Ça s’appelle un “spring-loaded plate dispenser” en anglais. Il permet de stocker des assiettes dans un espace assez compacte. Pourquoi est-ce que je vous parle de cette invention indispensable ?
D’abord parce qu’on en parle dans pratiquement tout livre de programmation C++ ou de programmation OpenGL (3d). mais surtout parce que ces livres n’ajoutent jamais d’images de ce fameux “spring-loaded plate dispenser”, alors nous avons fait l’effort d’aller en chercher-une…
Une des particularités du “spring-loaded plate dispenser”, c’est que la dernière assiette posée est la première retirée de la pile. Et c’est ce détail qui intéresse les programmeurs et nous ramène à nos deux méthodes pushmatrix() et popmatrix(). Quand on “pousse” (“push”) une assiette sur la pile elle enfonce la pile par son poids. Si on “retire” (“pop”) par la suite une assiette de la pile, c’est cette dernière qu’on retire, alégeant ainsi la pile de son poids.
De la même façon, chaque fois que nous voulons nous souvenir d’une position/orientation particulière de notre espace nous demandons au programme de “placer” (“pushmatrix”) cette position/orientation dans la mémoire. Si nous “plaçons” une autre position/orientation (“pushmatrix” encore) dans la mémoire, celle-ci si place au-dessus de l’autre.
Quand nous commençons ensuite à revenir en arrière, c’est-à-dire à “retirer” (“popmatrix”) des transformations, c’est la dernière placée sur la pile qui s’en va. Ce qui nous ramène à la précédente transformation. Si nous “retirons” (“popmatrix” encore) ensuite celle-ci, nous nous trouvons au point de départ, c’est-à-dire avec une fenêtre normale sans transformations.
Pour donner une illustration de cette idée, voici une autre animation interactive utilisant cette fois-ci plusieurs pushmatrix() accompagnés d’autant de popmatrix() :
float r = 0.0;
void setup() {
size(400,400,P3D);
}
void draw() {
background(255);
// se mettre au centre
translate(200,200,0);
// se souvenir de la position+orientation #1 (neutre)
pushmatrix();
// faire une rotation
rotateX(mouseY * 0.05);
rotateY(mouseX * 0.05);
// dessiner une boîte
fill(128,128,128,64);
box(20,20,20);
// se souvenir de la position+orientation #2
pushmatrix();
// se déplacer
translate(150,0,0);
// se souvenir de la position+orientation #3
pushmatrix();
// ajouter à la rotation
r += 0.05;
r = r % (PI*2.0);
// faire une rotation avec cette valeur
rotateY(r);
rotateZ(-r);
// dessiner une boîte
fill(255,0,0,192);
box(10,10,10);
// revenir à la transformation #3
popmatrix();
// dessiner une boite autour de la précédente
fill(128,128,128,16);
box(30,30,30);
// revenir à la transformation #2
popmatrix();
// revenir à la transformation #1
popmatrix();
}Ce code devrait vous donner quelque chose comme l’illustration suivante :
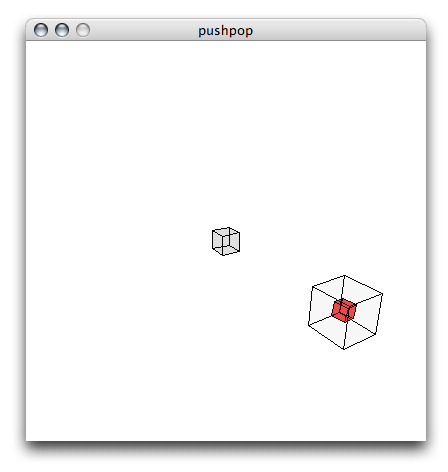
Notez que la petite boîte rouge tourne à l’intérieur de la plus grosse boîte grise. En plus, ces deux boîtes sont affectés par un déplacement à partir d’une orientation partagé par la boîte moyenne au centre. Cet enchaînement auraient été extremement fatiguant à programmer si on n’utilisait pas pushmatrix() et popmatrix(). maintenant imaginer ce qu’il faudrait comme complexité pour dessiner une forme dix ou cent fois plus complexe, comme celle d’une forme humaine. Sans ces deux fonctions, le programmeur seraient probablement perdu.
matrices
Nous n’allons pas rentrer dans tous les détails d’une matrice ici, ce n’est pas vraiment le lieu. Sachez néanmoins (si vous avez envie de les comprendre) qu’il s’agit d’un calcul mathématique permettant de donner une coordonée x, y, z en entrée et d’avoir en sortie la nouvelle emplacement de cette coordonée après manipulation par la matrice. Une matrice est une sorte de boite de transformation magique : on lui donne une valeur et il nous la transforme par la suite.
Comme c’est un calcul mathématique, l’ordinateur peut le faire très vite — pratique quand il s’agit de milliers de points à traduire.
Il y a trois manipulations matricielles qui sont souvent utilisés, parce qu’elle peuvent être calculées en fait par une seule matrice et donc en même temps : translate, rotate, scale. Ce calcul unique (multiplié pour chaque point, ligne, polygone de l’image) de ces trois paramètres permet à l’ordinateur de fabriquer des images complexes très rapidment. Ces trois transformations déplacement, orientation, et échelle sont en conséquence les trois transformations les plus importantes dans tout dessin 3d interactive.
On comprend aussi du coup l’importance de l’accumulation des transformations et leur gestion par les pushmatrix() et popmatrix(). Comme il s’agit tout simplement d’une forme de calcul proche de la multiplication, et que toutes les multiplications peuvent être simplifiées en les multipliant ensemble, il suffit de multiplier toutes les matrices dans le bon ordre (déplacement x rotation x déplacement x déplacement x rotation x rotation x etc…) pour avoir le resultat voulu. Le rôle de chaque pushmatrix() est de garder en mémoire ce calcul pour qu’il puisse le plus rapidement possible être appliqué à chacun des points cherchant à dessiner au bon endroit dans l’image.
Evidemment nous simplifions l’ensemble de ces procédés pour ne donner qu’une idée très général de l’activité de l’ordinateur, il n’empêche que ces concepts affectent la façon dont on construira l’image. Il est donc important de comprendre au moins quelque chose de ce processus, même s’il s’agit d’une compréhension assez sommaire.
Après tout, on n’est pas des mathématiciens. Si vous ne comprenez pas, ce n’est pas grâve (sauf pour moi : si on n’a pas bien compris, c’est souvent parce qu’on ne nous a pas bien expliqué). Tout ce qu’on veut faire, c’est de construire des formes et des images. Mais parfois il faut se faire chier travailler s’il on veut obtenir des résultats complexes. Heureusement, les cartes graphiques font la plupart de ce travail à votre place, et Processing s’occupe du reste. Vous n’avez pas à vous occuper des matrices en réalité. Il suffit juste de dire ce que vous voulez (un déplacement, une rotation, …) et Processing s’occupe du reste.
Dommage qu’on soit obligé de passer par des termes matheux comme pushmatrix() et popmatrix() pour y arriver.