Discrete computations in continuous planes

Via Slashdot who got it from tshb, here’s a fascinating paper by Daniel E. Holcomb, Wayne P. Burleson, and Kevin Fu (University of Massachusetts) on accessing the physical properties of digital circuits for both the generation of random numbers and the fingerprinting of individual circuits . The paper is entitled Initial SRAM State as a Fingerprint and Source of True Random Numbers for RFID Tags (link).

I always wonder why people are so obsessed with this idea of « true » random numbers. It’s as if computer science, in its vain lust for purity — i.e. to rid the circuitry of « noise » through the abstraction of physical substrates —, had somehow actually succeeded in achieving a purely unphysical world in which circuitry could conduct itself outside of the constraints of base material imperfection.

Ironically, the dream of true imperfection seems troubled by the same science fiction, only on the other side of the dialectic. For example, in John Maeda’s Design by Numbers, we find a similar disdain for the artificial nature of random numbers, and a gentle prod to new coders to avoid its siren song as much as possible :

The amateur may be tempted by the cheap thrills of randomness. Random numbers, noise, stochastics, or whatever you want to call the complete lack of control that serves as the roots of techno-styled graphics, is a form of profanity that you should generally avoid. But in many ways, resistance may prove futile because complete control of a complex computational process is still something of a faraway goal and the allure of randomness can be overpowering. My personal philosophy has been that if you are going to use randomness, you should at least know where it comes from. –Design by Numbers, p.247

I love Maeda’s pragmatism : hey Kid, before you play with that dirty code, you should at least know where it’s been sleeping around!

When I read that passage from Maeda’s 1999 masterpiece (yeah, that’s a big word, but come on, we’re talking about the origins of Processing here), I burst out laughing. Until then, I had avoided random numbers for pretty much the same reasons: they somehow represented sloppy, or lazy coding practices to me. But hearing someone else say it out loud immediately cured me of this folly and I immediately began throwing random numbers into pretty much anything that moved, calculated, reacted, beeped, blurped or just sat there waiting for someone to click on it. Upon learning that random numbers were the equivalent of an easy date, a vaccuous pop song, or perhaps the fatty delight of cheap fast food that you eat precisely because it is bad for you, somehow those random numbers felt all the more fun, all the more rebellious: kind of like dressing up like a punk rocker at 16 in the protected confines of your suburb (I know something about this): it’s not like you’re going to do any real damage to anything so you might as well just run with it.

But something funny happened after using these skanky random numbers for several years of guilty pleasure. Little by little I realized that I started to inuitively recognize these numbers and could even feel when my programs had shifted from one random thread to the next. I could even feel when my random numbers had moved from one dimension to two or three dimensions of calculation. Since most of the random numbers I used were of the really cheap kind (i.e. nothing like the relatively effective sort, such as the Mersenne Twister), ultimately I was coming to know (fairly well) the feel of the random number, even if its seed always departed from a new (and therefore different) point. It’s somewhat silly, I know, but in one project in particular — my Concrescence algorithmic cinema platform —, I actually stuck with cheap random numbers precisely because after so many years of milking those numbers I ended up finding what I considered their sweet spot of expression.

What I’m talking about, ultimately, is form; and it is this aspect which brings me back to the aforementioned paper. While the specifics may change, the forms they reveal are anything but immaterial. And just as in any process bound by what I like to call the process of algorithmic « physicalization », the effect is reversible. When I said that I felt my random numbers, I meant it quite literally as I was generating images and sounds based on user touch, and that material behavior became easy to recognize over time. You can understand a lot about the underlying physical apparatus that runs the software simply through the observation of its output. But the reverse is also true : by fiddling with the physical aspect of the cell you can impregnate digital circuits with interrestic behaviors.

I love the diagram on page 5 that follows this amazing quote: « By descending below the logical level of abstraction, and considering RAM to be a physical fingerprint, a wealth of information is found. » The diagram shows the precise point at which the SRAM cell generates both its fingerprint and « true » random numbers :

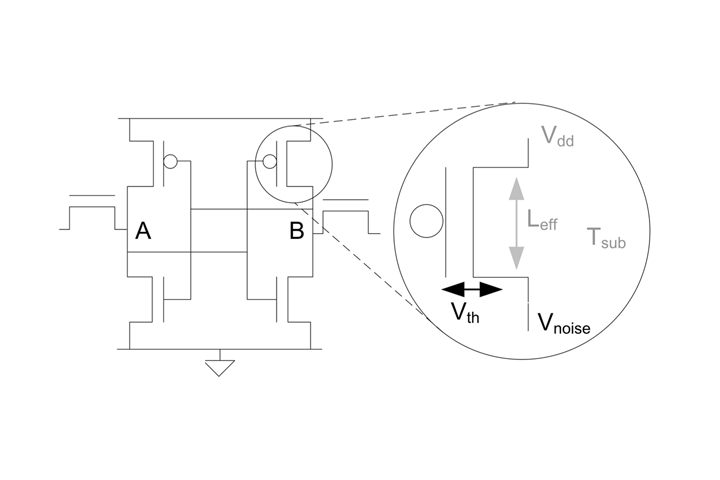
CmdrTaco expressed « surprise » at this double quality of {identification} and {randomness}. But when you get down to it, both states are by-products of the same nature of circuit being a physical device. To simplify our terminology, the circuit brings with it what so many today are calling « analog » world, although I find this term unfortunate because it merely exists as the rediscovered sibling of « digital ». I far prefer the idea of a process of physicalisation that poses the analog world as neither a given nor a goal, but instead an internal quality of hybrid processes.

The hybrid nature of repurposing digitally the physical circuit already sitting in the computer you’re using to read this post, is an exciting prospect, and if pushed to its extreme could even re-write the mythe du mite (the myth of the moth in the machine). When Grace Murray Hopper pulled that famous moth out of the machine and taped it into her notebook, the joke was of course that the idea of a « bug » in the machine had suddenly found a very litteral instance. But my reading of this myth went more into nature of interfaces, and the fact that the moth had actually crashed the machines precisely because it had interacted with the computer not via its terminal (or punch-card, or whatever), but instead directly via it’s modular circuitry. But in fact, technology such as random number generators that use the physicality of the circuit to determine a digital transduction, operate precisely at this level of « direct » interaction, and do so perfectly fine without crashing anything. And of course most transducers do the same day-in, day-out without causing any serious harm, and ultimately, as the referenced paper show, can be folded back into the digital nature of the circuit without much worry.