Lexique / variable

On those who enter the same rivers, ever different waters flow.
– Heraclitus ; The Fragments of Heraclitus ; pp. 12

Comme l’eau dans le célèbre fragment d’Héraclite, le mouvement interne de la machine informatique est en modulation permanente. Même si l’ensemble de la machine est composé d’états finis, chacun de ces composants discret se trouve sur un terrain en constant fluctuation.

It is not possible to step twice into the same river, nor is it possible to touch a mortal substance twice in so far as its state is concerned. But, thanks to the swiftness and speed of change, it scatters things and brings them together again, (or, rather, it brings together and lets go neither again nor later, but simultaneously) it forms and dissolves, and it approaches and departs.
– Heraclitus ; The Fragments of Heraclitus ; pp. 91

Paradoxalement, ces deux fragments d’Héraclite posent la possibilité d’une expérience de la mutation à partir de celle du même. Il se peut qu’en posant son pied deux fois dans le même fleuve nous nous rendons compte du changement qu’y a eu lieu, il n’empêche que cela suppose une continuité spatiale à l’endroit où nous posons le pied. Pour se rendre compte qu’il s’agit d’un fleuve différent, il faut présupposer néanmoins la possibilité d’un continuité temporelle dans l’espace.

Ce problème du changement face au même, du désir de trouver un endroit fixe depuis lequel nous pouvons nous rendre compte du changement, se règle dans l’informatique via l’introduction de la variable. Une variable informatique se représente souvent par une lettre, par exemple x, ou un mot, par exemple score. A « l’intérieur » des ses variable on attribue des valeurs :

x = -1;
score = 0;

Parfois, comme dans des environements tels que Pure Data, The Patcher ou Max/MSP, une variable est représentée par une sorte de boîte carré contenant un chiffre.

Et puis efin, il existe un troisième cas de variable comme par exemple une souris où il n’y a pas de chiffre visible, mais iù il s’agit néanmoins d’une variable contenant un chiffre. L’expression du chiffre se fait dans l’affichage du pointeur sur l’écran.

L’avantage de réprésenter des valeurs (-1, 0, 99, 666) par des mots ou objets graphiques est que les valeurs internes de ces représentations peuvent changer — d’où le terme « variable » — sans que le cadre de la représentation lui-même change. La valeur de la souris peut changer sans que la souris elle-même change de forme. De la même mannière, la valeur de la variable « score » peut changer (je peux agumenter tout d’un coup mon score de 200 points) mais pour le programmeur le mot qu’il ou elle doit manipuler reste le même : en demandant d’afficher le contenu de la variable « score » sur l’écran, l’ordinateur s’occupe tout seul d’afficher « 200 », « 300 », « -666 », ou « 42 » sur l’écran. Le programmeur n’a pas eu besoin de savoir la valeur de la variable au préalable. De cette mannière, un programmeur peut manipuler des entités (afficher le « score » sur l’écran, compter le nombre de fautes, etc) qui par nature sont flutuantes et donc inconnus d’avance. En plus, on peut changer nous-mêmes les contenus de telles variables sans savoir au préalable (au moment de l’écriture du programme) la valeur exacte de leurs contenus.

On isole la variabilité de la machine, en l’entourant d’au moins un paramètre dont on est sûr : nous ne connaîssons pas la valeur, mais nous savons au moins où elle se trouve. C’est le modèle spatiale de la machine qui permet cette prouesse de l’informatique : en spatialisant la logique nous rendons manipulables des logiques abstraites et variables. En cadeau, l’ensemble des composants de la même mannière se distribue dans des logiques spatiales (cf. mémoire).

Dans l’informatique le contrôle des fluctuations passe forcément par l’imposition d’une grille, et donc d’un repérage spatial. Chaque élement de la machine est considéré comme une modulation potentielle, mais repérable via son emplacement spatiale. Un régistre contient un ensemble fluctuant de valeurs, mais repérables par un emplacement spécifique et donc sondable. En plus, l’étendu des valeurs qu’ils peuvent contenir est limité, donc connu d’avance comme une gamme contrôlable. Pour revenir au fragment d’Héraclite, en replaçant son pied deux fois au même endroit on pourrait ainsi mesurer le changement du courrant entre les deux poses : en sondant deux registres de mémoire dans l’ordinateur à deux moment distincts temporellement, nous pouvons savoir par combien cet emplacement s’est écarté de sa valeur ancienne. C’est du moins la logique d’un ordinateur quand il s’agit de sonder un évenement en constant variation : en créant des entités fixes de modulation, l’ordinateur gère une infinitude de modulations potentiellement déstructives à sa structure carré.

cf. microphone

Diagramme. Une variable informatique délimite un espace fixe à l’intérieur de l’ordinateur qui contiendra par la suite des variations numériques. L’usage de ces valeurs numériques peuvent être de pratiquement n’importe quel ordre : une variable peut piloter un robots, agumenter/diminuer un son, ou générer un caractère alphanumérique sur un document. Mais à la base, la variable commencera toujours sa vie comme un chiffre dans un emplacement donnée. On délimite un espace, on le nomme — « x », « y », « score », etc — puis on commence à placer une valeur à l’intérieur.

L’usage d’une variable pour affecter toutes ces conséquences concrètes permet à l’ordinateur de maîtriser l’imprévu avec du prévisible. Elle lui permet également de créer des machines récursives de modulation d’une machine par une autre. En réduisant la complexité à des valeurs numériques, la machine peut se permettre ensuite une grande latitude dans les choix de communication et d’affectation transcursives (cf. Anti-œdipe, p.51-2) : la machine peut affecter une variable quelconque dans une séquence textuelle par une variable venue de la modulation d’une onde sonore. Comme les deux « objets » parlent la même langue (ils sont tous les deux des « variables ») la valeur de l’un peut facilement affecter la valeur de l’autre.

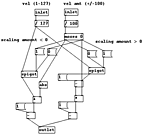
Dans le diagramme ci-contre, nous voyons une illustration plutôt simple de différents façons dont on peut se servir d’une variable. Il commence avec une variable unique constament réattribuée avec une nouvelle valeur qui corrépond à la position horizontale de la souris à l’intérieur de l’écran : quand la souris est plutôt à gauche dans la fenêtre cette valeur tend vers 0, alors qu’à droite elle tend vers 255. Il y a donc 256 différentes valeurs (255 + 0 = 256 différentes valeurs en informatique) qui corréspondent à la position horizontale de la souris. Cette valeur est affichée en haut du diagramme, avec une barre vérticale pour illustrer le rapport entre cette valeur et les coordonnées sur l’écran.

Dans les codes sources (cf. « variable.pde »), cette variable est représentée de la façon suivante :

x = mouseX;

Ce qui veut dire que 60 fois seconde la variable « x » prend comme valeur celle de la position horizontale de la souris.

En bas du diagramme, 16 usages de cette variable unique. La première case, par exemple, prend la valeur de la souris et l’inverse en utilisant la formule suivate :

x2 = 256 - x;

Avec cette formule, les valeurs de 0 à 255 de la souris deviennent des valeurs de 255 à 0 pour la variable « x2 ». Cette inversion sera ensuite appliquée à différents objets graphiques, par exemple la ligne verticale juste en dessous.

D’autres cases du diagramme illustre la façon dont une variable peut affecter le déplacement d’une autre variable. Dans la deuxième case, par exemple, cette variable « x » de la souris est utilisée pour déterminer l’étendu des valeurs aléatoires d’un carré qui frétille. D’autres cases, comme celle qui contient une ligne qui tourne en continu, utilise cette valeur « x » pour affecter le facteur de changement de sa propre valeur : la ligne a sa propre orientation, son propre « angle » qui est égalemment une variable ; mais la valeur « x » de la souris est ensuite utilisée pour moduler cette valeur. Au lieu d’utiliser la variable de souris comme une valeur fixe, elle est utilisée comme un valeur de modulation intermédiare. Cette médiation des variables dans la chaîne iterative du programme introduit une couche d’abstraction comme on peut en témoigner à travers des machines comme Vexation 1 d’Antoine Schmitt.

cf. microphone