Mode d'emploi. A gauche un simple jeu de Pong. Comme dans tout Pong, il y a une balle et deux raquettes. Cliquez pour lancer des balles (jusqu'à 16). Pour contrôller les raquettes, cliquez sur les boîtes de numéros affichés en bas : 128, 64, 32, 16, 8, 4, 2, 1. Chaque boite additionne sa valeur suivant la logique du bitmask et positionne la raquette à la position corréspondante.
Argument. Le « bitmask », ou « masque d'octets » est un concept informatique qui joue avec la nature spatial de l'ordinateur contre sa nature numérique. Le bitmask est une technique de programmation consistant à isoler séparément les « bits » d'un « byte » de mémoire — c'est-à-dire les huit unités qui composent un « octet » — et d'utiliser ces bits séparément comme des informations à part entière, ou en tout cas autrement qu'en tant que numéro.
Il est bien connu qu'un ordinateur ne sait compter qu'avec zéro et un. Parfois on entend qu'ensemble ces zéros et uns sont utilisés pour représenter des chiffres, d'où le terme « numérique ». Moins clair est ce que ça veut dire réellement.

Essayons d'imaginer le monde de la machine de son point de vue, c'est-à-dire comme une sorte d'hangar remplis de milliers d'interrupteurs microscopiques, chacun allumé ou éteint. On peut représenter ces interrupteurs avec des lumières clignotantes, des « blinkenlichten » (
Nous disons « symboliquement », car en réalité il y a trop d'interrupteurs à l'intérieur de la machine pour être représentés chacun par une lumière. Et d'ailleurs ils changent trop souvent et trop vite, jusqu'au point d'être impercetible s'ils étaient représentés par des lumières. Ces lumières donnent néanmoins une approximation de ce qui se passe à l'intérieur des machines comme activité.


Une autre approximation serait tout simplement de les représenter comme une suite d'interrupteurs, comme dans l'installation P2P de Gorbet Design qui physicalise la logique du « bitmap » et permet aux utilisateurs de changer l'état de chaque « bit » d'une image.
Mais la plupart de temps, ces interrupteurs sont réprésentés par des chiffres zéro et un, comme dans l'illustration suivant :

Chaque interrupteur est représenté par un chiffre dans un emplacement donnée. Si l'interrupteur est allumé il sera représenté par un « 1 »; s'il est éteint il sera représenté par un « 0 ». Ensemble il crée un champ complexe de chiffres appellés des « bits » (des « morceaux »). Décontextualisée, cette image représente une sorte de soupe, sans queue ni tête, une sorte de nuage de signes insignifiants. A l'intérieur de la machine, il s'agit physiquement d'interrupteurs microscopiques, mais dans la représentation que nous faisons de ces interrupteurs, il s'agit néanmoins de zéros et de uns; ceci pour des raisons très pratiques, comme nous verrons dans un instant.
Pour l'ordinateur, cette nuage de signes binaires est absoluement structurée. Décomposons par exemple la structure de notre exemple. Tout d'abord, il y a 1,440 zéros et uns, distribués dans 16 lignes de 90 chiffres. Et comme tout programmeur sait, tout chiffre à base de 16, 32, 64, etc. est parfaitement divisable en des sous-ensembles de 8, un des chiffres magiques pour la machine. Pour lire le contenu de notre soupe, il faut alors le décomposer en des sous-ensembles de 8.
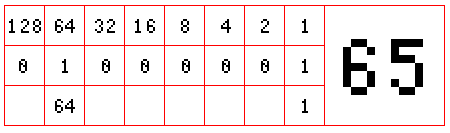
Prenons les huit premiers zéros et uns de la liste : « 01000001 ». Pour un programmeur expérimenté, comme pour la machine, il ne s'agit pas uniquement d'une suite de chiffres arbitraire, mais du chiffre 65, c'est-à-dire la lettre « A » de l'alphabet. Quoi? Comment sommes-nous arrivés à la lettre « A » à partir de « 01000001 » ? En attribuant des valeurs spatiales dans la chaîne, c'est-à-dire des significations particulières pour chacun de ses emplacements :
Chaque famille de huit chiffres traitera ses composants différement, selon leurs positions dans la chaîne. Comme dans un compte des frères Grimm, chaque chiffre joue un rôle différent dans l'histoire : l'aîné, le deuxième, jusqu'au petit dernier de l'histoire. Chaque position de la liste aura sa propre signification, voire sa propre valeur.
Dans notre exemple de la conversion de « 01000001 » en la valeur de 65 (c'est-à-dire la lettre « A »), il faut distinguer la valeur de chacun des « 1 ». Car chaque « 1 » ne représente pas forcément la valeur de « 1 ». Nous avons attribué à notre suite des puissances de 2 : 2^0=1, 2^2=2, 2^3=4, 2^4=8, 2^5=16, 2^6=32, 2^7=64, 2^8=128. De cette façon, nous pouvons exprimer jusqu'à 256 différents valeurs à partir d'uniquement 8 emplacements. La première case représentera une valeur de 128, ensuite la deuxième case représentera la moitié de cette valeur, c'est-à-dire 64, et ainsi de suite jusqu'à-ce qu'on arrive à la dernière case qui représentera la valeur de 1. En repérant quelles sont les cases remplis d'un « 1 » (plutôt que « 0 »), en multipliant ces cases par la valeur corréspondante (128, 64, 32, ...), et en additionnant tous les résultats, on arrive avec un chiffre entre 0 et 255. C'est la valeur maximale d'un octet : 255. Voici l'avantage de représenter l'interrupteur par la valeur de « 0 » ou de « 1 » : en les multipliant par 2^n on aura 0 x 2^n = 0 ou 1 x 2^n = 2^n. Chaque valeur devient « active » ou « nulle » suivant qu'elle est multipliée par 0 ou 1. On utilise l'astuce mathématique que toute valeur mulipliée par 0 égale 0 et que toute valeur multipliée par 1 est égale elle-même. N'importe quelle valeur peut être activée ou désactivée en allumant ou en éteinant un interrupteur.
Ici, pour notre huit premiers chiffres de la série, il s'agit de la valeur de 64 plus la valeur de 1, c'est-à-dire la valeur de 65. Si nous voulons la valeur unique de la suite de chiffres « 01000001 », elle sera donc 65. Et si nous cherchons la valeur 65 dans le tableau de signes alphanumériques « American Standard Code for Information Interchange » (ascii), nous voyons que la valeur 65 corréspond à la lettre « A » majuscule :

Avec rien que 8 petites cases d'interrupteurs, nous pouvons exprimer jusqu'à 256 différentes lettres alphanumériques.
Une fois que nous avons repéré cette logique de cadrillage des chiffres par suites de 8 chiffres — c'est-à-dire des « octets » de 8 « bits » - nous pouvons sectionner l'ensemble des chiffres et décoder leur « signification ». Dans notre exemple, si on prennait uniquement les dernières octets de notre nuage de zéros et de uns,

on arriverait enfin par lire dedans le mot « blinkenlichten », le dernier mot d'une célèbre panneau anonyme posé sur une machine informatique dans un laboratoire d'IBM dans les années 1950 (cf. « blinkenlichten » (
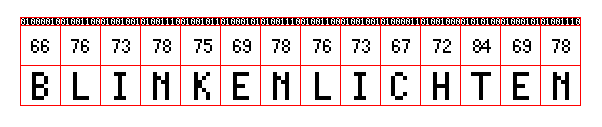
Tout cette information se tient dans des rangés d'intérrupteurs positionés « on » ou « off », « férmé » ou « ouvert », « 0 » ou « 1 ».
Maintenant que nous avons décrit le processus de transcodage d'une suite d'interrupteurs vers des valeurs numériques, prenons ce processus à l'envers. Imaginons que nous avons un chiffre ou une suite de chiffres — par exemple « 42 » —, et que nous voulons le converir en ses composants binaires :

Le résultat, comme on voit dans l'exemple est « 00101010 ».
Dans la définition informatique du « bitmask », la conversion aura lieu justemment dans ce sens d'une valeur numérique vers sa composition binaire. Le « bitmask » convertit un chiffre en des interrupteurs éteints ou allumés. Comme un masque qui ne laisse passer que les yeux, par exemple, le « bitmask » ne laisse passer que la partie de la chaîne qui nous intéresse. On peut lire l'état du bit no.1 indépendament du bit no.2, et ainsi de suite. On l'appele un « mask » à partir du moment où ces valeurs seront utilisées pour éxtraire de l'ensemble (de manière discrète) un ou plusieurs des « bits » individuel(s). Le procédé ressemble d'assez près à une forme de décodage d'un message codé, la révélation d'une logique proche du chiffrement, rappelant des liens forts entre l'informatique et la machine Enigma qu'Alan Turing cherchait à décoder pendant la deuxième guerre mondiale.
Le bitmask est utilisé dans divers opérations informatiques, mais sera privilégié surtout quand l'espace et les ressources de la machine ou du réseau sont réstreints. Si nous voulions commander un robot, nous pourrions éventuellement envoyer nos instructions à travers le réseau via des instructions lisibles par des êtres humains, genre « avancer », « reculer », « pousser sur la gauche », « tourner à droite », etc. Ces messages seraient donc lisibles pour nous et si on programme bien la machine ils seraient également lisibles par la machine. Par contre, ils seraient plus longues à communiquer au robot, plus gourmands en termes de ressources (surtout le temps nécessaire à les communiquer) et donc plus cher techniquement à mettre en place. On pourrait imaginer alors une sorte de codage spécial pour le robot, ou « a » singalerait au robot d'« avancer », « r » signalerait « reculer », et ainsi de suite. Du coup nous avons conservé par un facteur parfois de 20, la taille (et donc le prix/vitesse) de nos message.
Avec un bitmask nous pouvons conserver encore par un facteur de 8 la largeur de notre message, en envoyant en même temps huit instructions différentes dans un seul signe alphanumérique. Cette astuce profite du fait que presque toute communication ou calcul sur un ordianteur se fait en réalité avec des « octets » et non pas avec des « bits ». On cache à l'intérieur de cet octet les différentes instructions. Par exemple, en envoyant au robot le signe « * » (no. 42 sur le tableau ascii), on peut lui indiquer huit instructions indépendantes, empaquetées ensemble à l'intérieur d'une seul lettre du message. Ceci évite d'envoyer huit différents messages pour chacune des actions :

Comme on voit dans l'illustration, nous avons remplacé les valeurs « 128 », « 64 », « 32 », « 16 », « 8 », « 4 », « 2 », « 1 » de nos précédents exemples, par des mouvements : « se déplacer à gauche », « se déplacer à droit », « se déplacer en avant », etc. L'ordinateur regardera dans notre message la composition des interrupteurs utilisés pour représenter le signe, et les convertira en des instructions pour les moteurs. Comme toutes les communications se font avec des octets, nous pouvons cacher dans ces octets des informations discrètes dans chacun des huit bits. Du coup, en envoyant au robot un seul signe alphanumérique (« * » ou « 42 »), le robot se déplacera à droite et poussera tous les objets sur sa gauche et sur sa droite.
Pour nous, le bitmask joue le rôle de doubleur dans la machine, créant une information fantôme dans les interstices de chaque calcul, action, ou transmission de la machine. Dans cette logique de transcodage, n'importe quelle représentation dans la machine peut engendrer des actions ou de nouvelles représentations ailleurs dans la machine. Dans notre diagramme plus haut, la série d'interrupteurs discrèts, numériques contrôle les positions analogiques des raquettes en haut. Chaque interrupteur représente un bit, c'est-à-dire une partie de l'ensemble. En activant les combinaisons discontinus spatialement via les interrupteurs, nous arrivons à controller la position en continu de la raquette.
Sur le plan artistique, le transcodage du bitmask et sa mannière de doubler les informations ouvre des possibilités de juxtaposition pour le moins particulières. Ne serait-ce que dans le projet abstractmachine, nous avons utilisé le bitmask directement ou comme inspiration pour générer des combinaisons rhymiques musicales à partir d'une simple machine à écrire (cf. BitBox), où dans divers workshops tenus en 2001 où les déplacements de robots Lego Mindstorms étaient contrôlés par les couleurs de divers tableaux en suivant éxactement le procédé qu'on vient de décrire. Il suffit de disjoncter la réprésentation correcte, morale c'est-à-dire prédéstinée sémantiquement, et la remplacer par d'autres représentations qui peuvent à leur tour être disjonctées et utilisées pour générer encore d'autres actions ou représentations, et ainsi de suite.
En dehors des applications directes du bitmask — où la valeur d'un octet contrôle huit actions séparément — la logique de doublure de l'information suggère que toute interaction pourrait être doublée, voire triplée ou quadruplée par plusieurs couches actionnables. On peut créer ainsi des chaines de déroutage infinie, à la mannière d'un Duchamp et son La mariée mise à nu par ses célibataires, même (Le grand verre), mais cette fois-ci avec la possibilité d'actionneurs matériels. C'est surtout cette configuration — plus étendu que le simple bitmask à 8 bits — qui nous encourage comme espace à explorer sur le plan artistique, et que nous entendons comme principe moteur de la machine pour la création de machines abstraites.
cf. Rube Goldberg Machines, Jack Valenti Brings You efdtt, Color Typewriter, BitPong, BitBox, La mariée mise à nu par ses célibataires, même (Le grand verre)