- Artwork: Field-Works
- Artiste: Masaki Fujihata
- Lien: field-works
A l’inverse de .walk qui génère la forme de ses promenades à partir d’algorithmes, les Field-Works de Masaki Fujihata récupèrent des promenades déjà existantes et les utilisent pour les repromener à l’intérieur de simulations pour générer des algorithmes : des algorithmes captés, fixés par l’enregistrement des déambulations aléatoires des promeneurs. Petit-à-petit, on y voit apparaître la logique interne de ces promenades, qui ne sont finalement pas si aléatoires que ça (Fujihata construit ses promenades). Et ces promenades finissent par révéler des structures socio-topographiques — jusqu’a pouvoir révéler, par exemple dans « Field-Work@Alsace », la frontière franco-allemande. C’est à ce moment que la simple forme brute, le trait de la promenade enrégistré géographiquement, se remet à balader à l’intérieur de la simulation, et génère ce qui pour nous est un algorithme — algorithme car celui-ci est parfaitement reproductible et modulaire comme le démontre Fujihata en déclinant les multiples facettes possibles d’une même promenade.
Cette machine de Fujihata commence très simplement : une caméra vidéo qui enregistre, en plus de l’image et du son, des données à la fois spatiales du GPS mais aussi l’orientation x, y, z via des captures d’inclinaison. Cinq pistes synchronisées : image, son, position, orientation, le tout en relation avec le time-code de la cassette vidéo (la cinquième piste). Les fils de toutes ces données sont ensuite retissées à l’intérieur d’une machine de simulations en trois dimensions. Uniquement les données de l’enregistrement sont gardés : les photogrammes successives de la bande vidéo sont posés sur des « fils » vectoriels distribués dans l’espace suivant les données du GPS. L’orientation de la video sur cette ligne suit les données enregistrées par les capteurs d’orientation/inclinaison.
L’ingéniosité du « mapping » de Fujihata sur les composantes de la simulation 3d est à saluer. Dans les simulations à base d’OpenGL, les formes sont construites avec trois paramètres de « transformation » de la perspective avant la pose du pixel : le déplacement (« translation »), la réorientation (« rotation »), et les changements d’échelle (« scale »). Dans Field-Works, Fujihata calque les deux premières transformations directemment sur ses données, et même utilisera la troisième transformation dans une autre pièce (voir plus loin). C’est la calquage de ces transformations sur ces données qui forment l’image si particulière de Field-Works. Sans ces « transformations » chaque image des vidéos s’empileraient les unes sur les autres : toute image et tout dessin se ferait en deux dimensions comme sur un écran plat. Mais en calquant les transformations de déplacement sur les données directement du GPS, puis en calquant les transformations de rotation sur les données des capteurs d’orientation, on finit par distribuer chaque « frame », chaque image de la bande vidéo sur l’espace en 3D. Pour une illustration de ces manipulations voir le diagramme transform.

Plusieurs balades ont été fait avec cette machine. Dans « Field-Work@Alsace » (2002) Fujihata s’est baladé tout seul sur la frontière franco-allemande avec son appareil, enregistrant des témoignages des passants, tout en identifiant divers artéfactes spécifiques à cette condition transfrontalière, comme par exemple un petit pont piéton où chacun des côtés se trouvait dans un pays différent. La forme de la carte dessine plus ou moins une ligne, mais coupé par les allers et venues de Fujihata dans chaque pays de la frontière.
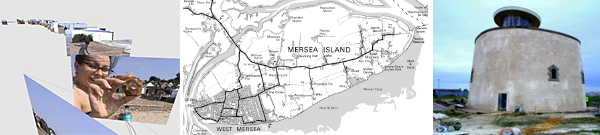
Dans « Field-Work@Mersea » (2003), Fujihata a donné ses caméras augementées à plusieurs groupes (150 personnes au total) qui sont parties dans des directions différentes pour parcourir L’île de Mersea et révéler la topoligie de l’île à leur manière. Parallèlement Fujihata est parti avec sa propre groupe pour faire tout simplement le tour de l’île. L’ensemble des enregistrements (image + son + GPS + orientation / temps) ont été ensuite réunis dans une carte dynamique interactive, mais également a été utilisé pour générer des topologies fabulatoires. Par exemple, en utilisant l’axe « temps » de l’enregistrement pour remonter progressivement la position des images sur l’axe vertical de la simulation, Fujihata a pu construire des spirales d’images; des spirales qui n’existait que par rapport à l’enregistrement, bien sûr, mais qui était néanmoins extraits des données bruts ramenés par les marcheurs.

D’autres expériences ont été tentées avec les Field-Works, comme « Field-Work@Matsue » (2002) où Fujihata et plusieurs assistants sur des bateaux (à moteur, à vent, à rames), des vélos et des transports en commun, ont filmés les bords du lac Shinji, faisant ainsi un portrait de l’intérieur et de l’extérieur du lac.

Pour les installations de Field-Works Fujihata fournit une interface d’interaction extrêmement simple : un grand bouton rotatif avec lequel l’utilisateur peut se promener en suivant les lignes de la déambulation enregistrée par la machine. Un peu comme un rouleau qu’on déroule dans un pianola, on circule sur les vecteurs de déplacement de enregistreurs. L’utilisateur construit ainsi ses propres points de vue sur ce terrain double de la simulation. La construction d’une forme à partir d’une série de données disparates est déjà intéressante en soi, et on trouve aujourd’hui de plus en plus de travaux (en tout genre) qui vont dans ce sens. Mais le fait de réintroduire la promenade à l’intérieur d’une machine à fabriquer de nouvelles promenades, génère une œuvre d’une toute autre nature : elle n’est plus démonstratif d’une forme déjà existante, elle est la matrice, le programme, de promenades à venir.
Déjà dans « Impressing Velocity », unes des toutes premières expériences de Fujihata avec le GPS, on voit la possibilité de faire plier la carte qui résulte d’une montée du Mont Fuji et générer ainsi de nouvelles cartes à partir de la première. Avec un GPS monté dans un sac à dos et relié à une caméra, Fujihata monte (et descend) le célèbre mont icônique avec des amis. Ensuite, une fois rentrée dans son laboratoire avec les données brutes (position + temps) Fujihata fait plier la carte selon les différentes vitesses de leur déplacements. Le déplacement rapide fait une contraction de la forme, alors qu’un déplacement lent produit des expansions. L’image d’un Mont Fuji fine au sommet est l’image de Fujihata et de ses amis en train de descendre à toute vitesse, alors que l’image presque biblique d’un Mont qui éclate en étoile à son apogée n’est rien d’autre que le résultat de la fatigue de la montée et d’une longue pause en haut pour déjeuner.

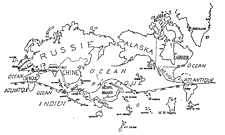
Cette carte est intéressante à juxtaposer, comme nous avons fait ici, à la carte des Surréalistes qui décrivent leur vision du globe sous l’œil surréaliste : La russie et L’alaska sont énormes, les États-Unis n’existent presque plus, flanqué maintenant par la « Labrador ». Elle montre la malléabilité des cartes selon différents critères qui nous sont toujours superposés : le point de vue, l’idéologie (cf. remap), l’imaginaire. Mais elle nous intéresse surout ici parce qu’elle annonce l’opération que Fujihata actionnera sur divers territoires par la suite. Elle démontre une des transformations que l’algorithme a fait subir à l’image : cette image n’est plus de l’ordre de la représentation, elle est indexique vis-à-vis d’une opération.
La pliure de la carte forme l’algorithme qui délimite les contours d’une action à faire sur la carte, sur le territoire, sur l’espace. On identifie ici cette pliure comme « algorithme » à cause de la nature diagrammatique de la pliure. Cette action est toujours à faire même si elle est déjà faite. Comme dans « Impressing Velocity » nous n’avons pas face à nous une simple forme, ou la simple « image » d’une carte déformée, ni une trace passive d’une intervention dans l’espace. La carte d’« Impressing Velocity » et de Field-Works n’est pas une image, c’est une carte des déformations qu’une déambulation a pu généré sur un territoire. C’est la carte d’une opération mais aussi la carte d’un potentiel. « Impressing Velocity » coule autant littéralement que figurativement : c’est une déformation en mouvement et les instructions pour une telle déformation, d’où l’usage du terme d’algorithme.
